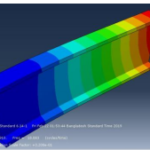
Structural Analysis of Continuous I Beam of Steel with Crack Using Finite Element Simulation
Mumtahina Rahnuma, Md. Mehadi Hassan Chowdhury, Nihal Ahmed, Ashfaq Ahmed
The statically indeterminate beam that is supported by three or more supports and at least one support that develops a reaction along the beam axis is known as a continuous beam. This type of beam is used in a large variety of structures as they show better resistance to seismic loads and lower deformity. However, due to the decay of steel or the increase of stresses, sometimes surface or sub-surface fissures develop in the material which is known as cracks. Because of the cracks in a structure, it may be vulnerable and start to age rapidly, which will eventually lead the structure to collapse. In this study, Abaqus CAE, a widely operated commercial software is used to simulate the cracks in a continuous I beam by the Finite Element Method. The surrounding crack zone is meshed with a smaller area due to its sensitiveness. Initially, suitable steel is selected among the major types of steel by evaluating their stress-strain curve. Then a continuous I beam of that steel with crack is simulated and the effect of the crack on the stresses is analyzed. The crack is safer when it forms on the part of the structure that is over-support. The risk of failure of a structure increases with the increasing distance of the crack from support. The greater crack depth poses a greater risk to the structure on the other hand increasing crack width has less effect on the stability of the structure

A Finite Element Analysis of Automobile Leaf Spring
Shahriar Hasan, Ashfaq Ahmed, Nihal Ahmed, Muntasir Mamun
Leaf springs are a special kind of springs and are one of the most important components of an automobile suspension system. Leaves are basically a series of flat plates, usually of semi-elliptical shape. Generally, a multi-leaf spring used in automobile suspension consists of two types of leaves i.e. graduated length leaves and full-length leaves. The advantage of leaf spring over heli-cal spring is that the ends of the spring may be guided along a definite path as it deflects to act as a structural member in addition to energy absorbing device. The main function of leaf spring is not only to support vertical load but also to isolate road induced vibrations. It is subjected to millions of load cycles leading to fatigue failure. The static analysis determines the safe stress and strain of the leaf spring and to study the behavior of structures under practical conditions. Our present study attempts to analyze the safe load of the leaf spring. It also validates the concept of cantilever beam employed in the theoretical analysis of multi-leaf spring. A lot of research work has been carried out in the context of leaf spring considering its material and significant progress has been observed in the field of weight reduction, and improvement of load-carrying capacity under the replacement with any advanced material. Finite element analysis has been carried out to determine safe stresses and payloads. The multi-leaf spring was modeled in SOLIDWORKS 2015 and the same were analyzed under similar conditions using ANSYS Workbench 19.2 software considering structural steel and SAE 1074 spring steel as the spring material. Theoretical and software-based results are presented and compared for validation. Dimensions are taken from the multi-leaf spring used in the vehicles in Bangladesh.

Vibration Response Analysis of a Structural Metal Mild Steel under the Effect of Crack
Nihal Ahmed, Ashfaq Ahmed, Muntasir Mamun
When a crack is present in a structure then the probability of failure of that structure is higher. Failure occurs when the natural frequency of the periodic force and the natural frequency of the structure are in a state of superposition. To avoid this phenomenon, it is essential to calculate the natural frequency. The aim of this study is to analyze the behavior of natural frequency for different parameters such as crack position, crack depth, crack opening and mesh sensitivity. In this study, the first five modes of vibration of both cracked and uncracked I beam has been extracted. A further analysis of resonance for a fixed vertical load has also been done. An amalgamation of hexahedral and wedge elements has been used to study the behavior of the cracked structure. As this is a problem of discontinuity, thus it is very troublesome to make a solution analytically. Therefore, ‘ABAQUS CAE’, one of the most popular finite element analysis software, was used for the analysis of cracked structure. The discoveries of this examination are that the presence of crack decreases the natural frequency of the beam, this decrease is identified with the position of the crack, its opening and its depth. Another finding of this examination is that the impact of vibration is huge for I beam when the break arrives at its web segment. It was also discovered that resonance happens before if the crack profundity is bigger or the existence of the crack is nearer to the fixed end.
Comparative Study of Different Implicit Finite Difference Methods to Solve the Heat Convection–Diffusion Equation for a Thin Copper Plate
Nihal Ahmed, Ashfaq Ahmed, Muntasir Mamun
Finite Difference Implicit methods have been frequently used for solving the heat convection-diffusion equation. One of the biggest advantages of implicit schemes is that the solution remains well behaved for arbitrarily large time steps. Crank Nicolson and Alternating Direction implicit and Alternating Direction semi-implicit methods are very popular finite difference methods. They have been previously applied in many heat convection-diffusion problems. In this paper, we use these finite difference implicit methods to solve the heat convection-diffusion equation for a thin copper plate. By comparing the results obtained by these methods we determine the best method for solving problems related to heat transfer of a thin plate. The results depict that the Alternating Direction method provides the most accurate and stable solution. Crank Nicolson method is suitable for large scale solution and the Alternate Direction semi-implicit method requires less computation time but provides detritus solution in the x-direction.
